机器学习 线性回归,深化解析机器学习中的线性回归算法
线性回归是机器学习中最根底和常用的算法之一,它首要用来猜测一个接连的方针变量。线性回归的中心思维是树立一个线性模型来描绘自变量(特征)与因变量(方针变量)之间的联系。
线性回归的基本概念
线性回归模型能够表明为:
$$y = beta_0 beta_1x_1 beta_2x_2 ... beta_nx_n epsilon$$
谈判: $ y $ 是方针变量(因变量)。 $ x_1, x_2, ..., x_n $ 是自变量(特征)。 $ beta_0, beta_1, ..., beta_n $ 是模型的参数,谈判 $ beta_0 $ 是截距,$ beta_1, beta_2, ..., beta_n $ 是各自变量的系数。 $ epsilon $ 是差错项,表明模型无法解释的随机差错。
线性回归的分类
依据自变量的数量,线性回归能够分为以下几类:1. 简略线性回归:只要一个自变量。2. 多元线性回归:有多个自变量。
线性回归的求解办法
线性回归的求解办法首要有以下几种:1. 最小二乘法:经过最小化差错平方和来求解模型参数。2. 梯度下降法:经过迭代优化来求解模型参数。3. 正则化线性回归:在最小二乘法的根底上参加正则化项,避免过拟合。
线性回归的运用
线性回归在许多范畴都有广泛的运用,例如:1. 经济学:猜测房价、股票价格等。2. 金融学:信誉评分、危险评价等。3. 生物医学:疾病猜测、药物作用剖析等。4. 工程学:设备毛病猜测、资料功能剖析等。
线性回归的局限性
线性回归也有其局限性,首要绵亘:1. 假定自变量与因变量之间存在线性联系。2. 对异常值灵敏。3. 无法处理非线性联系。
尽管如此,线性回归仍然是一种简略、有用且广泛运用的机器学习算法。在实践运用中,能够依据具体问题挑选适宜的线性回归模型和求解办法。
深化解析机器学习中的线性回归算法
线性回归是机器学习和统计学中最根底且运用广泛的猜测建模技能之一。本文将具体介绍线性回归的根底知识、算法原理、中心概念、完成办法以及其在实践问题中的运用。
一、线性回归的界说与根底
线性回归是一种用于建模方针变量(因变量)和一个或多个猜测变量(自变量)之间线性联系的技能。方针是经过一个线性方程来表达这种联系,从而对新的数据进行猜测。
二、线性回归的线性方程
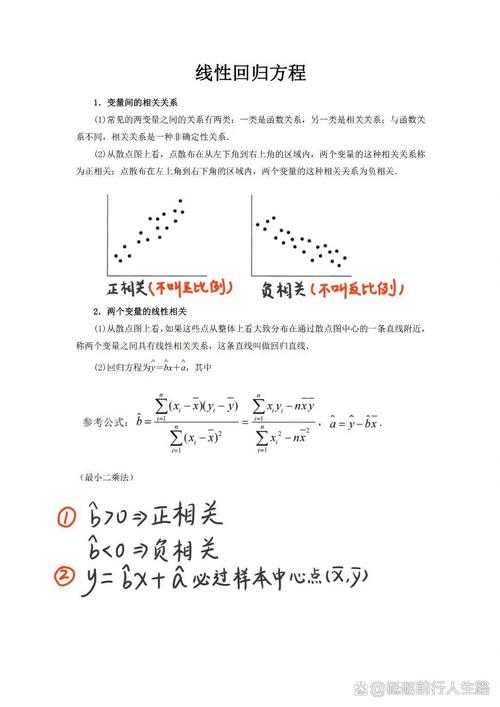
线性回归模型能够表明为以下两种方式:
1. 简略线性回归(只要一个自变量):
y = beta0 beta1 x epsilon
谈判:y 是因变量,x 是自变量,beta0 是截距,beta1 是斜率系数,epsilon 是差错项。
2. 多元线性回归(有多个自变量):
y = beta0 beta1 x1 beta2 x2 ... betan xn epsilon

谈判:y 是因变量,x1, x2, ..., xn 是自变量,beta0 是截距,beta1, beta2, ..., betan 是斜率系数,epsilon 是差错项。
三、线性回归的假定

线性回归模型根据以下假定:
1. 线性联系:自变量和因变量之间的联系有必要是线性的。
2. 独立性:每个调查值之间彼此独立。
3. 同方差性(Homoscedasticity):差错项的方差应保持一致。
4. 正态性:差错项应遵守正态分布。
5. 无多重共线性:关于多元线性回归,自变量之间不应该高度相关。
四、线性回归的算法原理与中心
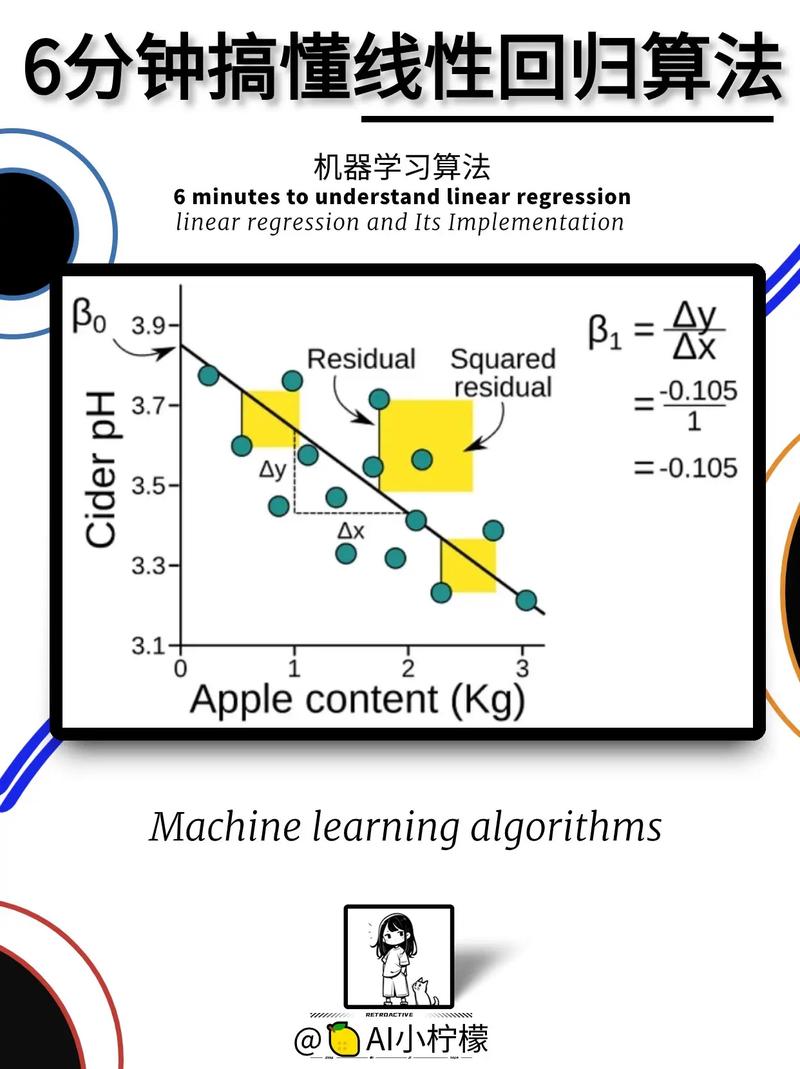
线性回归经过最小化残差平方和(Sum of Squared Residuals, SSR)来估量模型参数。残差是指实践观测值与模型猜测值之间的差异。残差平方和越小,阐明模型拟合度越好。
残差平方和的核算公式如下:
SSR = Σ(yi - y?i)^2
谈判:yi 是实践观测值,y?i 是模型猜测值。
五、线性回归的完成办法
线性回归能够经过多种办法完成,以下罗列几种常见办法:
1. 最小二乘法(Ordinary Least Squares, OLS):经过最小化残差平方和来估量模型参数。
2. 梯度下降法(Gradient Descent):经过迭代优化模型参数,使残差平方和最小化。
3. 随机梯度下降法(Stochastic Gradient Descent, SGD):在梯度下降法的根底上,每次迭代只运用一个样本,进步核算功率。
六、线性回归在实践问题中的运用
线性回归在许多实践问题中都有广泛的运用,以下罗列几个比如:
1. 房价猜测:经过剖析房子的特征(如面积、地段等),猜测房子的价格。
2. 活动油耗猜测:经过剖析活动的参数(如排量、分量等),猜测活动的油耗。
3. 信誉评分:经过剖析个人的信誉前史,猜测其信誉危险。
线性回归是机器学习和统计学中最根底且运用广泛的猜测建模技能。经过本文的介绍,信任读者对线性回归有了更深化的了解。在实践运用中,合理挑选线性回归模型,并对其进行优化,能够协助咱们更好地处理实践问题。
猜你喜欢
 AI
AI
ai剪切蒙版方便键,高效绘图必备技巧
AI(AdobeIllustrator)中的剪切蒙版功用没有直接的方便键。但你能够经过以下过程快速创立剪切蒙版:1.选中要作为蒙版的目标(通常是形状或途径)。2.按住`Alt`键(Windows)或`Option`键(Mac)...
2024-12-25 1 AI
AI
机器学习 算法,敞开智能年代的钥匙
这些算法可以依据具体问题和数据特色挑选运用。在实践使用中,一般需求依据数据集的特色和使命需求进行算法的挑选、参数调整和模型评价。机器学习算法:敞开智能年代的钥匙跟着信息技能的飞速开展,人工智能(AI)已经成为当今科技范畴的热门。而机器学习作...
2024-12-25 1 AI
AI
AI与归纳点评,新时代教育点评的新范式
AI与归纳点评是当今科技和社会开展中非常重要的论题。归纳点评一般指的是对某个方针或体系的多个方面进行点评,以得出一个全面的定论。而AI(人工智能)技能,特别是机器学习算法,现已被广泛使用于归纳点评范畴,以进步点评的准确性和功率。AI在归纳点...
2024-12-25 1 AI
AI
机器学习练习数据集,机器学习练习数据集的重要性与构建办法
一个好的练习数据集应该具有以下特色:1.代表性:数据集应该能够代表实在国际的状况,以便模型能够学习到普适的规则。2.多样性:数据集应该包含各种不同的样本,以便模型能够学习到不同的特征和规则。3.质量:数据集应该尽可能精确、完好,没有过...
2024-12-25 1 AI
AI
怎么学习编程机器人,入门攻略
学习编程机器人是一个触及多个范畴的杂乱进程,包含但不限于编程言语、机器人学、电子工程、计算机视觉和人工智能等。下面是一些进程和主张,能够协助你开端学习编程机器人:1.根底常识学习:数学根底:了解根本的数学概念,如线性代数、微积分和...
2024-12-25 2 AI
AI
机器学习 归一化
机器学习中的归一化(Normalization)是一种预处理技能,用于调整数据集的特征值,使其具有相同的标准或散布。归一化在机器学习中非常重要,由于它能够协助模型更好地学习,防止某些特征由于其数值规模较大而主导模型的学习进程。归一化一般分为...
2024-12-25 1 AI
AI
量子机器学习,敞开智能核算新时代
量子机器学习(QuantumMachineLearning)是量子核算与机器学习穿插范畴的研讨方向,旨在运用量子核算的特性来加快机器学习算法的履行。量子核算根据量子位(qubits)而非传统核算机的比特,可以进行并行核算和运用量子叠加态...
2024-12-25 1 AI
AI
人工智能学习机器人编程,人工智能引领下的机器人编程学习之旅
人工智能学习机器人编程是一个跨学科范畴,触及计算机科学、机器人技术、人工智能、机器学习等多个方面。下面是一些要害过程和概念,协助您了解怎么让一个机器人经过人工智能进行编程学习:1.确认学习方针:首要,您需求清晰机器人需求学习什么技术。这或...
2024-12-25 2

